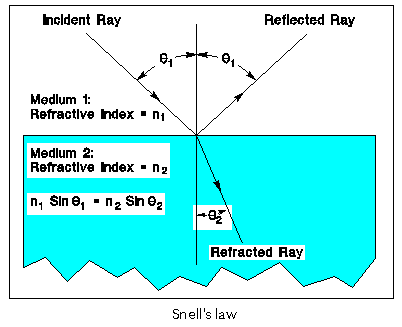
Snell’s law
A law of geometric optics that defines the amount of bending that takes place when a light ray strikes a refractive boundary, e.g., an air-glass interface, at a non-normal angle. Note 1: Snell’s law states that 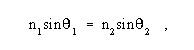 where n1 is the index of refraction of the medium in which the incident ray travels,
where n1 is the index of refraction of the medium in which the incident ray travels, 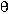 1 is the angle, with respect to the normal at the refractive boundary, at which the incident ray strikes the boundary, n2 is the index of refraction of the medium in which the refracted ray travels, and
1 is the angle, with respect to the normal at the refractive boundary, at which the incident ray strikes the boundary, n2 is the index of refraction of the medium in which the refracted ray travels, and 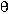 2 is the angle, with respect to the normal at the refractive boundary, at which the refracted ray travels. The incident ray and refracted ray travel in the same plane, on opposite sides of the normal at the point of incidence. Note 2: If a ray travels from a medium of lower refractive index into a medium of higher refractive index, it is bent toward the normal; if it travels from a medium of higher refractive index to a medium of lower index, it is bent away from the normal. Note 3: If the incident ray travels in a medium of higher refractive index toward a medium of lower refractive index at such an angle that Snell’s law would call for the sine of the refracted ray to be greater than unity (a mathematical impossibility); i.e.,
2 is the angle, with respect to the normal at the refractive boundary, at which the refracted ray travels. The incident ray and refracted ray travel in the same plane, on opposite sides of the normal at the point of incidence. Note 2: If a ray travels from a medium of lower refractive index into a medium of higher refractive index, it is bent toward the normal; if it travels from a medium of higher refractive index to a medium of lower index, it is bent away from the normal. Note 3: If the incident ray travels in a medium of higher refractive index toward a medium of lower refractive index at such an angle that Snell’s law would call for the sine of the refracted ray to be greater than unity (a mathematical impossibility); i.e., 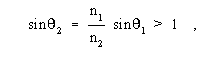
then the “refracted” ray in actuality becomes a reflected ray and is totally reflected back into the medium of higher refractive index, at an angle equal to the incident angle (and thus still “obeys” Snell’s Law). This reflection occurs even in the absence of a metallic reflective coating (e.g., aluminum or silver). This phenomenon is called “total internal reflection.” The smallest angle of incidence, with respect to the normal at the refractive boundary, which angle will support total internal reflection, is called the “critical angle.” [After FAA]